Sometimes, if you do not begin at the end, you end at the beginning (Ginat, 2005).
Backward thinking in problem solving can be observed frequently in my life and design career, either happening to me or some one else. I have learnt many lessons about it and want to write about it here.
Following are the definitions of forward and backward thinking (terms thinking and working can be used interchangably).
Working forwards is the way of approaching a problem by starting from initial state and advancing forwards, towards the goal state (Polya, 1957 in Ginat, 2005).
Working backwards is the way of advancing backwards from the goal state (Polya, 1957 in Ginat, 2005).
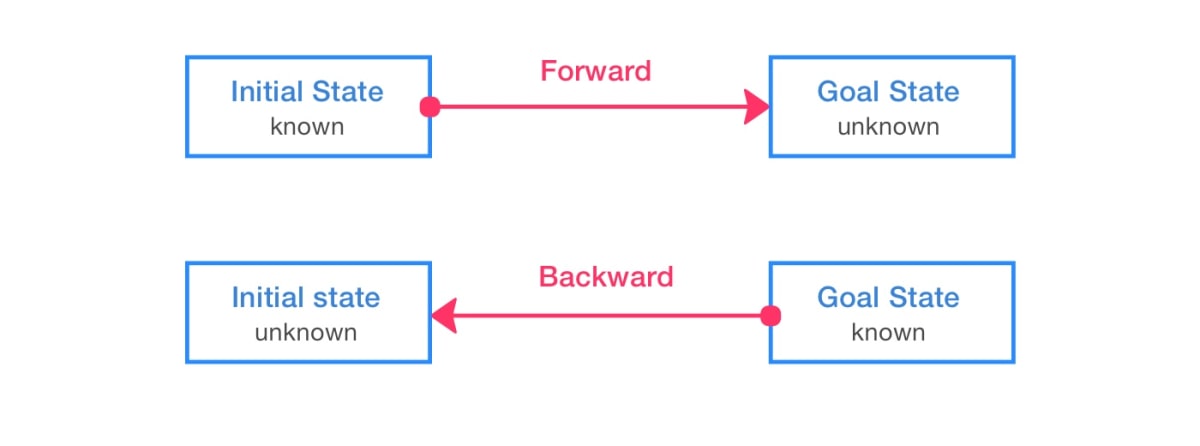
The goal state can be defined by you, and presence sometimes is not fully known as you thought.
It is easy to see why people often choose the forward option: from Initial state to Goal state. However, the reverse might be more logical and often optimal. People tend to think they understand what they have at the presence and constrain themselves to that understanding when planning for the future. Without defining the desired goal, it’s easy to limit yourself and miss out ambitious targets.
When designing a new product, people start from it being a sucess and work backward what they need to achieve to reach that goal. However, other people prefer to look at the past performance and current state of product and work forward what success they might reach. We will compare these two ways in the subsequent articles of this series. You have used backward thinking before
Though fancy as it sounds, backward thinking is what you actually have used since you were a kid. Remember the last time you lied to someone? For example, when you didn’t come on time. You started with not coming on time, went backwards to seek excuse and settled with reason that there was a traffic jam. Your friend might have asked why she shared the same route and didn’t see any traffic jam. You started with the fact that she didn’t see the jam and thought backward to seek another explanation.
Math is one of the first domains where we learn how to work backward. Let’s consider two following math problems:
-
Problem 1: A car park has a maximum capacity of 75 cars. What is 2/3 of its capacity?
-
Problem 2: A car park currently has 50 cars parking. We know that this is only 2/3 of its maximm capacity. What is its maximum capacity then?
In the first problem, 75 cars is the known initial state, the relation to goal state is operation with 2/3. The solution is times 75 and 2/3, which is working forward.
In the 2nd probem, 50 cars is the known goal state, the relation to maxium capacity (unknown initial state) is 2/3. The solution is to know 1/3 of maximum capacity first and then derive the whole, which is working backward.
Why I care about Backward Thinking?
As more and more people, including me, say we are problem solvers, I reflected and recognized gaps in my knowledge and skills required to solve problems, especially in UX design. I decided to learn problem solving from foundation. I started with which concepts and framework people use to solve problems in case studies. The next step is to undersand those concepts and frameworks. Problems requiring backward thinking like problem 2 mentioned earlier represent many case studies I have read.
Exercise
After knowing the concepts of backward and forward thinking, I reflected on what happened in my past projects and notice that I used both methods under different circumstances.
In the next article, I’m going to talk about starting project with objectives, instead of problems. Meanwhile, you can start looking at how you solve daily problems from perspective of working forward and backward. Prepare to be surprised!
References
Ginat, David. “The suitable way is backwards, but they work forward.” Journal of Computers in Mathematics and Science Teaching, vol. 24, no. 1, 2005.